Cada modelo de Machine Learning resuelven los problemas con distintos tipos de objetivos utilizando un conjunto de datos, por lo tanto las métricas de regresión en aprendizaje automático es importante tratar de comprender toda la información previa antes de escoger una métrica apropiada para poder tener los mejores resultados.
Para poder determinar cual es la mejor opción para resolver un problema debemos realizar el siguiente cuestionamiento.
- Cuál es el giro del negocio?
- La distribución de la variable objetivo
- El tipo de clasificación Regresión o Clasificación
Las métricas de regresión determinan problemas del modelado predictivo lo cual implica la predicción de un valor numérico.
Al utilizar el tipo de clasificación hay que tomar en cuenta que implica predecir mediante una etiqueta de clase, NO se puede utilizar las métricas de clasificación para evaluar las predicciones realizadas por un modelo de regresión.
Para poder resolver, se debe utilizar métricas de error las cuales están diseñadas para poder evaluar predicciones realizadas en problemas de regresión.
Cuales son las métricas de regresión?
- (MSE) – Error cuadrático medio
- (RMSE) -Error cuadrático medio
- (MAE) -Error absoluto medio
- (R²) – R al cuadrado
- R cuadrado ajustado (R²)
- (MSPE) – Error de porcentaje cuadrático medio
- (MAPE) – Error porcentual absoluto medio
- (RMSLE) – Error logarítmico cuadrático medio
Solución para las métricas de regresión
Las métricas de error, se puede resolver siguiendo los siguientes pasos:
- Modelado predictivo de regresión.
- Evaluación de modelos de regresión.
- Métricas de regresión.
- Error cuadrático medio. (MSE)
- Error cuadrático medio. (RMSE)
- Error absoluto medio. (MAE)
Modelado predictivo de regresión
El modelado predictivo de regresión consiste en determinar y desarrollar un modelo utilizando datos históricos y con estos poder realizar una predicción.
Se puede describir como un problema matemático para la aproximación de mapeo de funciones, utilizando variables de entrada y variables de salida, esto quiere decir (X) para las variables de entrada y (Y) para variables de salida.
La variable de salida que necesitamos encontrar es un valor real o un valor de punto flotante.
Evaluación de modelos de regresión
Al intentar pensar en un modelo de regresión, tomando en cuenta la precisión, nos inclinamos por un modelo de clasificación, pero en este caso la precisión de la clasificación es una medida de clasificación, no de regresión.
Lo mas importante en la evaluación de los modelos de regresión, es tener la habilidad de informar como un error en esas predicciones.
Existen tres tipos de métricas de error que se usan para la evaluación y el reporte del desempeño de un modelo de regresión.
- Error cuadrático medio. (MSE)
- Error cuadrático medio. (RMSE)
- Error absoluto medio. (MAE)
Existen varias métricas de regresión, pero las expuestas aquí son las más utilizadas, se puede revisar más información de la biblioteca de aprendizaje automático de Python de scikit-learn.
Métricas de regresión
En esta etapa con las métricas de regresión, se analizarán las métricas de error más utilizadas.
Error cuadrático medio. (MSE)
Posiblemente es la métrica más simple, pero igual es probablemente la menos útil.
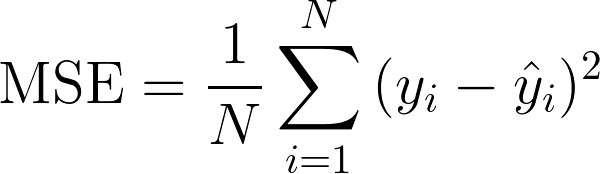
El error cuadrático medio MSE, mide el error cuadrático promedio de las predicciones para cada punto, calcula la diferencia cuadrada entre las predicciones y el objetivo esperado para luego promediar los valores.
Mientras mas alto sea el promedio peor es el modelo, para este promedio no puede ser negativo, para que la predicción sea exacta, el valor debe acercarse a cero y para ser perfecto debe ser cero.
Se puede revisar más información de la biblioteca de aprendizaje automático de Python de sklearn.metrics.mean_squared_error.
y_true = [3, 0.5, 2, 7]
y_pred = [2.5, 1.1, 2, 8]
from sklearn.metrics import mean_squared_error
mean_squared_error(y_true, y_pred)Error cuadrático medio. (RMSE)
Básicamente el error cuadrático medio (RMSE) es la raíz cuadrada de error cuadrático medio (MSE), se introduce la raíz cuadrada para que la escala de los errores sea igual a la escala de los objetivos.

En la práctica, la raíz del error cuadrático medio (RMSE) se usa más comúnmente para evaluar la precisión del modelo. Como su nombre lo indica, es simplemente la raíz cuadrada del error cuadrático medio.
y_true = [3, 0.5, 2, 7]
y_pred = [2.5, 1.1, 2, 8]
MSE = mean_squared_error(y_true, y_pred)
RMSE = math.sqrt(MSE)
print("Error cuadrático medio. (RMSE):",RMSE)Error absoluto medio. (MAE)
El error absoluto medio (MAE), este tipo de error se calcula como un promedio de diferencias absolutas entre los valores objetivos y las predicciones, el error absoluto medio es una puntuación lineal, lo cual significa que las diferencias se ponderarán por igual en el promedio.

El error absoluto medio (MAE) se usa principalmente en las finanzas, se puede tomar como ejemplo un error de $20 es exactamente el doble de peor que el error de $10.
y_true = [3, 0.5, 2, 7]
y_pred = [2.5, 1.1, 2, 8]
from sklearn.metrics import mean_absolute_error
mean_absolute_error(y_true, y_pred)